Esta entrada es una traducción adaptada de A mathematician in quarantine. Flattening the curve, and why you should stay at home, publicada originalmente en el blog del Netherlands eScience Center.
Escribo esto al comienzo de la crisis del COVID19 en Europa. No soy médico, de modo que el lector no encontrará aquí ningún consejo de salud ni sobre cómo sobrellevar estos días extraños. Lo que sí soy es matemático (o algo parecido). Si sientes curiosidad por cómo los epidemiólogos hacen predicciones acerca de la evolución de una enfermedad infecciosa, este texto quizá la satisfaga.
Probablemente hayas oído que el número de infecciones está creciendo «exponencialmente». Aunque en el lenguaje común «exponencial» parece significar «más rápido que ayer», en lenguaje matemático tiene un significado mucho más preciso. Tanto, que existe toda una rama de las matemáticas dedicada a estudiar la progresión de enfermedades infecciosas: la epidemiología matemática. Y las curvas son mucho más interesantes que exponenciales. Aquí veremos uno de sus modelos más básicos.
Modelo de Kermack – McKendrick
El modelo más célebre de propagación de una enfermedad es el de Kermack y McKendrick, y data de 1927. Se le suele llamar modeo SIR, debido a los nombres de sus tres variables de estado:
- S: la población de individuos susceptibles (de contraer la enfermedad)
- I: la población de individuos infectados
- R: la población de individuos recuperados
El modelo tiene este aspecto:

Pero no te dejes amilanar por las ecuaciones. Es posible entender los detalles de este modelo matemático usando una imagen mental: la de unos tanques de agua colocados como en la figura de más abajo. In esta figura, toda la población está en el «tanque suceptible». Nadie está infectado, de modo que nadie puede contagiarse y todo va bien.

¿Qué sucede si aparece una enfermedad? Esto es, ¿qué pasa si la población de infectados no es cero? Pues… que se abren los grifos.
Las ecuaciones de más arriba no son más que una descripción de cómo de abierto o cerrado está cada grifo. En particular, el grifo de arriba sirve para vaciar el «tanque de susceptibles», y para llenar el «tanque de infectados». Ese maldito grifo representa el contagio, y la magnitud de su flujo, r·S·I , es mayor cuanto mayor sea la cantidad de gente susceptible e infectada (piensa en ello, ¿tiene sentido?). La constante r representa la velocidad relativa de contagio, y será más alta para enfermedades más contagiosas. El grifo de abajo vacía el «tanque de infectados». Su flujo tiene una magnitud de a·I, de modo que a representa la tasa de recuperación relativa. Ver imagen más abajo.
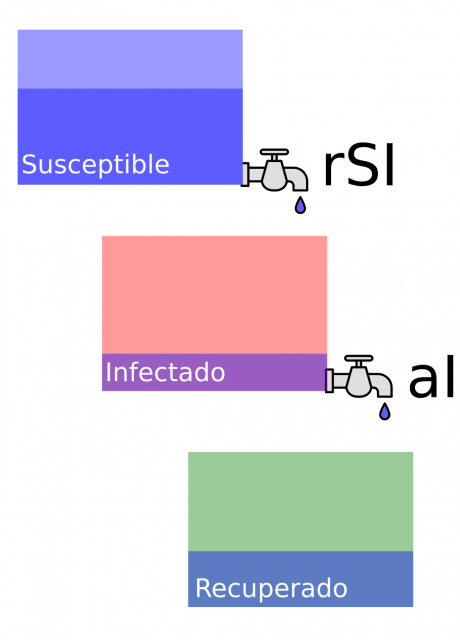
Con esta imagen en mente, las ecuaciones de más arriba cobran vida (fíjate que si el grifo vacía el tanque, su flujo correspondiente será negativo).
¿Y qué pinta tienen las soluciones?
Pues eso dependerá de la cantidad inicial de susceptibles, infectados y recuperados. Y sobretodo, de los valores de los parámetros r y a. Clickando en la imagen puedes acceder a una simulación interactiva (código fuente aquí).

¿Y esto para qué sirve?
El modelo SIR es un modelo extremadamente sencillo para un fenómeno muy complejo (si quieres más, echa un ojo a este artículo de Francis). Aún así, nos enseña un par de lecciones valiosas. Jugando con las tasas de contagio (r) y recuperación (a) la forma de las curvas cambia.
No es difícil imaginar que reducir r (menor tasa de contagio) y/o aumentar a (mayor tasa de recuperación) será bueno. Su efecto principal es aplanar la curva de contagio (la de color rojo), distribuyendo el número de casos en el tiempo y evitando así una potencial saturación del sistema sanitario. ¡Abre el applet interactivo y compruébalo tú mismo!
¿Y cómo aplanamos la curva? Bien, aumentar a (la tasa de recuperación relativa) no está en nuestras manos todavía, pues de momento no hay cura para el COVID19. Una vacuna podría reducir enormemente la población susceptible, … pero todavía no existe tal vacuna. Lo que sí está en nuestras manos es reducir r (la tasa de contagio), quedándonos en casa y minimizando nuestras interacciones sociales.
Te lo ha dicho tu madre, te lo han dicho tus amigos, te lo dicen las autoridades y ahora te lo dicen las matemáticas: quédate en casa.
Mucha fuerza para todos.

Referencias
- Kermack, W. O. and McKendrick, A. G. “A Contribution to the Mathematical Theory of Epidemics.” Proc. Roy. Soc. Lond. A 115, 700–721, 1927.
- Las matemáticas vigilan tu salud. Clara Grima y Enrique F. Borja.
- Murray, James D. Mathematical Biology I. An Introduction. 3 Vol. 17. New York: Springer, 2002.
- Este y otros modelos más elaborados pueden verse en Wikipedia y en La ciencia de la mula Francis


Eres un especialista en todo lo que te pongas… Un abrazo de tu tita… Ángela
Si pero en esto veo que mi problema no soy yo que a veces veo que tengo que ir a la tienda de comestibles, o la farmacia, sino aquellos que se te acercan, incluso si te reconocen de algún sitio se te abalanza para abrazarte,desearte buena suerte etc.
Acá, como en muchos lados no se consiguen barbijos, incluso se duda de su eficacia pues permtirian el paso del virus, la mejor prueba que tienes para decidir que no sos portador es no haber tenido fiebre, no toser, no haber estado con alguien que hubiera estado en Italia en las últimas semanas, y por supuesto uno no puede estar pidiendo que le muestren el pasaporte y tratando de leer la fecha de ingreso, o declaración de con quien durmió los últimos dias.
1 Del artículo se desprende la importancia de detectar los contagiados cuanto antes y separarlos de los no contagiados para hacer mínimo en el tiempo y en el número de afectados (sanen o mueran) el efecto de la ya declarada pandemia.
2 En la práctica no ha habido hasta la fecha (25-03-20) y no tiene pintas de que vaya a haber en unas semanas una implementación MASIVA (por lo menos a todos los sintomáticos y a colectivos de riesgo) de test de diagnóstico que permitan ese triaje eficaz.
3 ¿Por qué a pesar de saber no se actúa de forma consecuente?…por mucho que lo intento «racionalizar» siempre llego a la conclusión de que hay fuerzas inexplicables que provocan movimientos incomprensibles, marxismo (Groucho)puro: plantean (quienes sea que lo hacen)problemas para los que proponen soluciones falsas y acaban tomando medidas inadecuadas…
Se debe escribir separado sobre todo y sin tilde aun así.
Buen artículo.