Ayer publiqué un tuit que, contra todo pronóstico, tuvo bastante éxito. Digo contra todo pronóstico porque el tuit trataba nada menos que de integrales y derivadas. Decía lo siguiente:
¿Qué edad tenías cuándo te enteraste de que la integración por partes y la regla del producto son lo mismo? [link]
La integración por partes es ese «truco» para integrar funciones «complicadas» que a casi todos nos enseñaron en el instituto. La fórmula tiene el siguiente aspecto:

y solía ser un quebradero de cabeza memorizarla. Un truco muy común para no olvidarse del orden de las us y las uves era usar la frase: un (u) día vi (dv) una (u) vaca (v) vestida (v) de uniforme (du).
Por otro lado, la regla del producto nos dice que la derivada del producto de dos funciones es la suma de la derivada de la primera por la segunda sin derivar, más la derivada de la segunda por la primera sin derivar. Frases como esta son la razón por las que es mejor usar fórmulas:
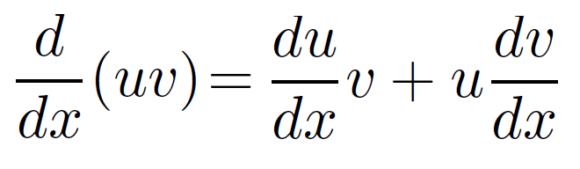
De las respuestas que recibí, aprendí dos cosas:
- Que muchísima gente conoce la surrealista historia de la vaca, pero no tantos saben que esta fórmula es lo mismo que la regla del producto para derivadas.
- Que mucha gente responde en serio a preguntas retóricas.
Como hubo quién me pidió aclaraciones, aquí dejo una explicación más desarrollada en cinco pasos:

- Escribimos la regla del producto. Por comodidad, la he escrito de derecha a izquierda.
- Hacemos algo que pone muy nerviosos a los matemáticos: multiplicar a ambos lados por el diferencial dx.
- Integramos ambos lados.
- La integral de una suma es la suma de las integrales. La integral de un diferencial es el interior del diferencial (más constante de integración, pero ignoremos eso de momento).
- Despejamos la integral de u dv y, voilá.
Si, con esto y con todo, prefieres memorizar la fórmula, te aconsejo que la memorices como en el paso cuatro:
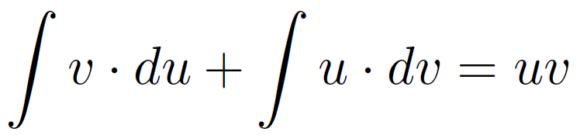
¿La razón?: esta fórmula es completamente simétrica. Si intercambias u y v, sigue siendo correcta. O lo que es lo mismo, si te equivocas y confundes u con v, no metes la pata.
Bola extra: Si la integración por partes y la derivación de un producto son lo mismo, ¿es posible integrar usando sólo la regla del producto? La respuesta es sí. Si te interesa, échale un vistazo a mi colaboración con Gaussianos: Integrando por partes like a boss.


Prefiero
S U sanita un D ia V ió U n V istoso S oldado V estido D e U niforme
…….perdonadme por poner las diferenciales con D, Esta frase a mi suena al siglo XIX, soldaditos de la WWI, niñas y nodrizas. Yo soy friqui y viejo, Qué mal rollo!
JJSJSJAJ amé
Un día ví una vaca sin cola vestida de uniforme
U*V fx=x² raíz de x-1
Sorry me quedo con la vaca vestida de uniforme!!!
Cuando empieces con integrales te va a encantar
Cuando dices ‘regla del producto’ sería más correcto decir ‘regla de la derivada de un producto’ …
no se entiende nada
mejor opción dejar bachillerato 🙂
ennove
8===>
Bryant Myers
Hoy de nuevo te voy a ver
Si llaman, pichea el cell (Almighty)
‘Tamos fumando marihuana
Hoy serás mi esclava en el cuarto de un motel
Hoy de nuevo te voy a ver, estoy bien bellaco
Quédate en pantys, modélame en tacos
En lo que yo enrolo y desenmoño el saco
Me quito el pantalón, por el boxer lo saco
Tengo un par de retros, me visto bien caco
Te gusta en la cama cómo te maltrato
Quieres que te lo meta a cada rato
Cuando está sola jugamos al ratón y al gato
Yo bajo sin peros, yo soy el bombero
Que te apaga el fuego en tu desespero
Me gusta lamberte los dos agujeros
Me gusta tu cara cuando entra entero
La mejor que me lo ha hecho, si te soy sincero
Echa la cachispa en el cenicero
La máquina que vibra y no es la del barbero
Déjame descansar, ya terminamos el primero
Me mira y me dice que la lleve a la nota máxima
Que la hipnotice
Que nada más con tocarla yo tengo el poder
De lograr que la piel se le erice
La vaca
Quiere Coco Chanel, Louis V, Bottega (Coco), yeah
La puse en 69, no a la amiga (mmm)
Ese culo tan lindo y tú con novio, baby, eso no pega
Baby, eso no pega
Chingamo’ con mis prenda’ puesta’, quedó ciega (ice, ice, ice, ice)
Yeah, preguntan por mí y ella lo niega
Nunca sale, pero si es por mí ella le llega (ella le llega)
Ya me acosté a dormir, pero si es pa’ chingar levántame (¡Hey!)
Tengo chavo’ con cojone’, chapéame (cash, cash, cash)
Yo sé que tú también, perdóname
No fue el destino, nah, fui yo que te llamé
Qué rica te ves en mini, trajecito bikini (damn)
Ferrari, uh, no le gustan los Lamborghini (skrrt, skrrt)
Mucha pasta, Carbone, fetuccini
Las de escorpio son peligro, lo dijo Mela y Rukmini, ey
Una demon, la monté en el Rolls-Royce (¡Eh!) y le puse YOVNGCHIMI (wuh)
Yo no soy malo, nah, bebé, eso e’ un gimmick
Pero el sol de PR calienta má’ que el de Phoenix
Ella lo sabe, pa’ Milán de compra’, despué’ pa’ Rimini
San Marino
(Todo por debajo ‘el agua, submarino)
Las moña’ multicolor cristalino
Le quité los Valentino, nos fuimo’, despué’ se vino (¡Hey!)
Mala, mala, ey
La puse mala
Los polvo’ en la sala
En el baño me escala
Se te regó la máscara
I don’t know, yo no sé nada, je
Yo no sé nada
a
Depílate y úntate el splash de chocolate
Entra al yate y relájate, y desnúdate
Ese totito a ti te late, y ese culote (y ese culote)
A ti te gusta chingar conmigo, na má’ desde que te derroté, mai
Aféitate la tota, porque hoy te lo vo’a meter
Te compré el traje Versace que valía mil tre’
Uno’ panti’ Victoria’s Secret, bebé
¿En qué paí’ tú quieres amanecer?
¿Te quieres ir por el mar en el yate
O nos vamos volando en el jet?
Aféitate la tota porque hoy te lo vo’a meter
Te compré el traje Versace que valía mil tre’
Unos pantis Victoria’s Secret, bebé
¿En qué paí’ tú quieres amanecer?
¿Te quiere’ ir por el mar en el yate
O no’ vamo’ volando en el jet? (good morning)
Hoy despertamo’ fumando en Californi
Bebé, ¿qué tú quieres beber?
Yo bebo champán, yo no bebo McCormick
Yo sé que a ti te gusta forni
Cuando tú te sienta’ horny
Toa’ mi’ prendas son de oro, yo no uso zirconi
Hoy te lo voy a meter
En el yate o en el jet
En la mansión o en el chalet
Ten el pelo y la’ uña’ set
deja de usar mi nombre
Pablo Rodríguez (Guadalajara, España, 1984) se siente inclinado de un modo casi suicida hacia las cosas complicadas. Esta cualidad le ha llevado a convertirse en físico, malabarista, ilusionista aficionado y humorista de cuarta categoría. Actualmente trabaja como experto en computación científica en el Netherlands eScience Center. Más información aquí
Voy flow leyenda
Como Madonna en los 90′
Cuando entro yo cierran la tienda
La pasarela tiembla
La T y la E no inventan
Pero, cuando se apaga la TV, eh eh eh eh eh
Se siente bien portarse mal, ah ah ah ah ah
Nos vamo’ a desconocer
Hoy vos vas a conocer
La version original, ah ah ah ah ah
Porque ahora que nadie nos ve, eh eh eh eh eh
Vamo’ hacerlo profesional, ah ah ah ah ah
No’ vamo’ a desconocer
Hoy vos vas a conocer
La version original, ah ah ah ah ah
Flash, flash, pose, pose
Mira mi cara en portada de Vogue
Diva Argentina, doy clases de flow
Ya es mucho tiempo acá arriba en el top
Stop, pongo los dramas en off
Mientras vos le pones play a mi song
No tengo tiempo, no sé ni quien sos
Yo solo veo mi gente en el show
La Alemania nazi o Alemania nacionalsocialista, conocida también como el Tercer Reich, es el término historiográfico común en español para referirse al Estado alemán entre 1933 y 1945, durante el gobierno del Partido Nacionalsocialista Obrero Alemán y su máximo dirigente, Adolf Hitler, al frente del país.
Francisco Franco Bahamonde fue un militar y dictador español, integrante de la cúpula militar que dio el golpe de Estado de 1936 contra el Gobierno democrático de la Segunda República, dando lugar a la guerra civil española. Wikipedia