Las ecuaciones diferenciales son una de las pesadillas clásicas de todo estudiante. Por lo general, uno se topa con ellas en los primeros años de cualquier carrera técnica.
Si eres estudiante y te estás peleando con este tipo de ecuaciones, el applet que presento en este post te puede resultar interesante. En él podemos visualizar (y manipular) el utilísimo concepto de slope field o «campo de direcciones» para una ecuación diferencial del tipo:
El truco para dibujar un campo de direcciones consiste en interpretar la ecuación diferencial como una receta que, a cada punto del plano (x,y), asigna una derivada (dy/dx). Dibujando una serie de pequeñas rectas, orientadas según la derivada correspondiente a la posición que ocupan, podemos hacernos una idea visual de cómo se comportarán las soluciones, que, como sabrás, deben ser tangentes a todas las rectas por las que pasen. Por así decirlo, es como si la ecuación diferencial llenase el plano con «señales» de tráfico indicando a la curva hacia dónde moverse a cada paso.
En la caja superior izquierda se puede introducir la función f(x,y) que uno quiera (si se desea, se pueden incluir hasta dos parámetros en ella). Arrastrando los puntos verdes se modifican las condiciones iniciales, y las curvas mostradas son soluciones numéricas a la ecuación diferencial. Se permite representar dos soluciones diferentes.
Lo mejor es jugar un poco con él. En algunos ordenadores puede correr un poco lento. Una alternativa es descargar el original y abrirlo con GeoGebra.
Este artículo forma parte de la sección Ciencia interactiva. El material original está disponible en GeoGebraTube


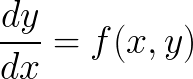
Muy bueno y muy interactivo. 🙂
¡Hola! Soy yo otra vez. Solamente quería decir que me ha encantado tu charla en Naukas 2016. Sabes hablar muy bien y enganchas. Por cierto, mi futurólogo preferido se llama «Método de Runge-Kutta de 4º orden» : P Un saludo.
Felicidades creo que has creado una herramienta bastante potente. La ec dif. y’=5*cos²(y*x) – y² – 5 no encuentro ninguna otra calculadora que lo haga!!! Lástima que no se pueda ampliar ni reducir la escala…
Gracias, Marc. Para hacer cosas más finas como cambiar escalas, te recomiendo que descargues el applet original (https://www.geogebra.org/m/u3VRk9Ab) y lo abras con GeoGebra, ya sea en su versión online o escritorio (ambas gratuitas).
Muchas gracias, Pablo!
Hola Pablo, soy yo otra vez. No se si acabo de entender bien la asignatura pero me gustaría saber de alguna ecuación diferencial en la que dada una condición inicial (o sea un par de puntos (x0,y0)) exista más de una solución.
El problema es que no se como interpretarlo. Probablemente al solo ver una porción del espacio es como si la condición de función Lipschitz pasase a ser localmente Lipschitz lo que hace que por el Teorema de Picard muchas de las funciones que en R^2 tienen más de una solución, aquí solo se vea una.
Supongo que la gracia seria buscar una solución cuyo compacto de Lipschitz sea tan pequeño que se pueda apreciar que existan dos o más soluciones por un par de puntos.
Muchas gracias.
Marc
Hola Marc,
muy buena pregunta. Respuesta rápida: si (x0, y0) es un punto de equilibrio, muchas soluciones convergerán hacia este. De modo que si te doy solamente el punto, no puedes decidir a qué solución pertenece. Esto se ve mejor en el
plano de fases.
Por cierto, yo también tengo una pregunta para ti: he notado que mis applets de ecuaciones diferenciales han tenido un subidón de visitas recientemente. ¿Alguna idea de a qué se puede deber?, ¿quizás os los han recomendado en clase?
Un saludo y gracias por tu interés.
Creo que soy yo que las visito 40 veces al día! Realmente son super útiles. Las he recomendado mucho. Muchas gracias por haberlas hecho