De vez en cuando recuerdo mis tiempos en el instituto (y según el día también me echo al suelo en posición fetal al recordarlos). Por aquel entonces, las matemáticas se convirtieron en mi asignatura más odiada y, muy a menudo, suspendida. Como muchos otros estudiantes, me topé con ese par de pesadillas matemáticas que, como el hombre del saco, dejan de asustarte a partir de cierta edad. Me refiero a las derivadas y las integrales. Hoy hablaré solamente de las primeras, y que no se asuste nadie, a pesar de las fórmulas, no resolveré ni desarrollaré nada… simplemente hablaré de su aspecto.
Decía Richard P. Feynman que:
Las matemáticas son, en gran medida, el arte de inventar notaciones mejores.
Se trata de una frase muy apropiada para alguien que inventó un modo gráfico, bastante útil, limpio e incluso estético, de interpretar las interacciones entre partículas subatómicas. Pero no nos llevemos a engaño… no hace falta acudir a las altas cimas de la física de partículas para encontrar ejemplos en los que una buena notación puede facilitarnos la vida, o una mala dificultárnosla innecesariamente. Si no me creen, prueben a hacer multiplicaciones con lápiz y papel, pero usando números romanos.
Volviendo a mis problemas con las derivadas, recuerdo que, tras muchos quebraderos de cabeza, descubrí que un simple cambio de notación mejoraba enormemente mi rendimiento en los ejercicios: se trataba de la conocida como notación de Leibniz. Quizá con ese nombre no suene muy familiar: ¿qué tal notación «de primas» y notación «de diferenciales»? La siguiente figura ayudará a refrescar la memoria:
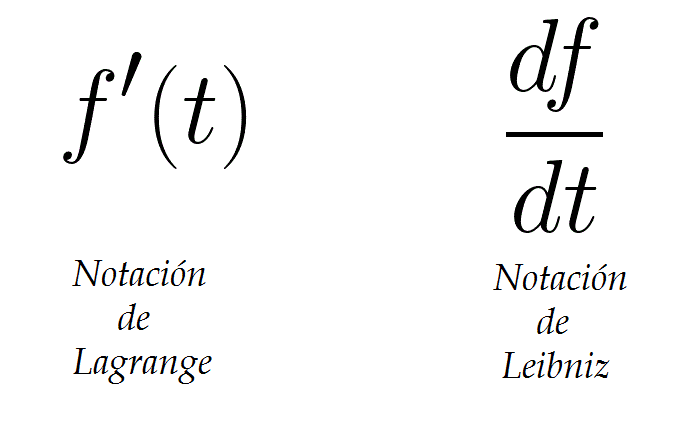
Por motivos que jamás comprenderé (agradezco si alguien arroja algo de luz en los comentarios) los libros de texto de bachillerato de matemáticas utilizaban notación de Lagrange, mientras que los de física utilizaban notación de Leibniz.
Llegados a este punto mis lectores pensarán algo como: «¡No me jodas Pablo!, ¿en serio tienes una opinión apasionada sobre notaciones?» Pues en efecto, la tengo; es más, me considero un auténtico hooligan de la notación de Leibniz. Muy especialmente cuando se trata de enseñar a derivar a principiantes como el que yo fui. Expondré mis motivos:
La notación de Lagrange es una rareza: solamente se usa para derivadas de funciones de una variable. Para integrales y funciones de varias variables se usa siempre la notación de Leibniz, de modo que vas a tener que aprenderla te guste o no. ¿Sabes qué pinta tiene una integral en notación de Lagrange?, probablemente no, porque apenas se usa. Si sientes curiosidad, mira la figura a continuación:

Quizá el lector recuerde que el diferencial (dt en el ejemplo anterior) jugaba cierto papel a la hora de hacer integrales. Hasta el punto de que existe un método, el de integración mediante cambio de variable, que obliga a hacer ciertas operaciones con él. Pues bien, esto también es cierto (y esencialmente por los mismos motivos) en el caso de las derivadas, como veremos en el siguiente apartado.
La regla de la cadena es sencillísima usando notación de Leibniz: este es sin duda el motivo más importante. La mayoría de ejercicios de derivación a los que se enfrentan los estudiantes no son difíciles, pero son enrevesados. Exigen la aplicación sucesiva de varios pasos sencillos. Uno de los métodos que más quebraderos de cabeza causan es el de la regla de la cadena, usado para derivar funciones compuestas. Veamos un ejemplo mínimo:
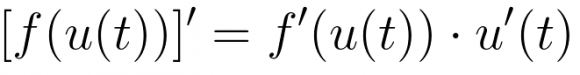
Para empezar, escrita así es una regla difícil de recordar. Además, en cada caso, el símbolo » ‘ » significa derivada respecto a una variable diferente. La misma regla, escrita en notación de Leibniz, tiene este aspecto:

Escrita así resulta no solo más fácil de recordar (parece un producto de fracciones en las que ambos du pueden eliminarse), si no también de aplicar, sobretodo cuando es necesario aplicar varias veces de forma sucesiva:

Usando la notación de Lagrange el ejemplo anterior tendría un aspecto realmente enrevesado.
La notación de Leibniz permite definir un operador independiente. La notación de Leibniz es mucho más cómoda a la hora de definir un operador derivada, en abstracto:

¿Y para qué me sirve a mí un operador abstracto?, pensará el lector. Pues para algo bastante útil cuando te atascas en mitad de un examen: tomarte un respiro en mitad de un ejercicio. Cuando tienes que hacer una derivada larga, no es fácil escribir pasos intermedios usando notación de Lagrange, sin embargo con la notación de Leibniz puedes dejarte un buen trozo sin derivar y colocar el símbolo delante… para atacarlo después.
La notación de Leibniz es más cercana a la definición de derivada. Esto más que una razón es un por qué. Si echas un vistazo a lo que realmente es una derivada, verás que su estructura contiene una fracción:
Es esta semejanza estructural de las derivadas con la notación de Leibniz es la que explica que, de forma natural, muchas propiedades de las derivadas se expresen de forma más clara con esta notación.
En resumen: ¡usa Leibniz, coñe!
Me interesa también vuestra opinión, ¿qué notación preferís para derivar?, ¡adelante con los comentarios!
Para más información sobre estas y otras notaciones aún más marginales, recomiendo este artículo de Wikipedia (en inglés): Notation for differentiation


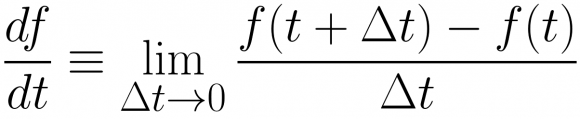
«los libros de texto de bachillerato de matemáticas utilizaban notación de Lagrange, mientras que los de física utilizaban notación de Leibniz.»
Yo creo que el motivo es este: la notación de Leibniz da la impresión de que una derivada es el cociente de dos cosas muuuy pequeñas. Los matemáticos se suben a las paredes cuando oyen eso. Pero es que sí lo es, y si no lo es, como si lo fuese. Poner f’ da la impresión de que una dericada es otra cosa. Los físicos somos más pragmáticos. Si parece un cociente, funciona como un cociente y se opera como si fuese un cociente… tampoco hay que romperse mucho el coco.
Estaba por decirlo, profesor.
A los cuasi ingenieros no pasa algo parecido, nos preocupa menos la belleza de una ecuacion que su resultado practico y su rapida resolucion.
Pero no es un problema de todos los matematicos.
En el siglo pasado, cuando ya tayudito me decidi por volver a estudia la ingenieria, me dieron unos libros de matemática basica que no osare mentar, salvo por su descomunal coste.
Por entonces tenia amistad con un profesor de matematicas de la USC y le consulte la materia, mas que nada porque la tenia muy olvidada — yo tambien me pongo en posicion fetal chupando el pulgar, e incluso me meto bajo la cama —, el me dijo, despues de hojearlo con creciente estupor, que no sabía quien lo habria escrito pero que sus explicaciones y desarrollos no los entendia ni el.
Ni que decir tiene que la asignatura provocaba muchas posiciones fetales y fecales en aquel primero.
Y no, no tenia mucho que ver con la escasa preparacion de los alumnos novatos.
Me temo que la cuation es que algunos autores se sumergen tan profundamente en su ciencia que pierden la capacidad de comunicar su conocimiento en terminos asimilables por los mortales.
Y por desgracia, sientan escuela.
Debo añadir, que para mi tambien eran bestias negras, pero le doy la razon en su postulado, yo tambien entiendo — no mejor, simplemente la entiendo y eso es mucho — esta notacion.
Un saludo.
Exacto, me gustó su comentario.
No soy ni físico ni matemático, sino ingeniero y me he sentido totalmente identificado tanto con el artículo como con el comentario de Arturo Quirantes.
Personalmente necesito utilizar la notación de Leibniz y me resulta muy, pero que muy difícil seguir cualquier cálculo que use la de Lagrange.
Qué le vamos a hacer, limitado que es uno.
Los matemáticos somos unos vagos, en la notación de Lagrange se escribe sustancialmente menos.
La regla de la cadena en notación de lagrange, está mal escrita, Pablo:
[f(u(t)]’=f'(u(t))·u'(t).
OJO
Llevas razón. Arreglado.
Gracias 🙂
Y ya puestos, está la notación del punto arriba de Newton (la de las fluxiones).
Para trabajar como función, es muchísimo más útil la notación de Lagrange.
Ahora, si sois unos mediocres que os conformáis con las simples aplicaciones de las derivadas como son las ecuaciones diferenciales, por supuesto que debéis usar la Notación de Leibnitz.
Pero recordad, que en ese caso, sólo estáis mirando una parte minúscula del poderío de las derivadas.
Fisicuchos… 😉
El espacio partido por el tiempo en cinemática no es la velocidad, es la velocidad media. De la misma manera, en matemáticas la derivada no es un cociente (eso en todo caso es la pendiente); es un límite. La potencia de dicho concepto radica precisamente en esto, en que es una razón de cambio INSTANTÁNEA.
En este sentido, para entender bien el concepto de derivada, antes hay que tener claro los límites o el concepto de diferencial. Para personas que se inician en el análisis matemático el primer concepto es mucho más asequible que el segundo. Es por ello que como definición para ellos, considero más acertada la de Lagrange. Sin embargo si considero necesario para apoyarse y para que entiendan bien el concepto, hacer también mención a la notación de Leibniz.
Y en cuanto a su uso, depende. Me quedo con todo lo señalado por el maestro Eliatron y en especial con su corrección de la regla de la cadena.
Fisicuchos…. Jejejeje.
La derivada es el limite de un cociente, lo que, prácticamente la haría un cociente también.
Te voy a mandar al tío la vara!
Todo bien, hasta que dijiste «fisicuchos»
Pues yo abogo por la notación de Euler, que tiene las ventajas de la de Lagrange, las ventajas de la de Leibniz y encima es próxima a la notación del cálculo vectorial.
Estoy de acuerdo, pero tiene un problema: es con diferencia la más minoritaria de todas.
Injusto, pero es un problema.
En Teoría de Operadores es la que se utiliza.
Estoy de acuerdo en que la notación de Leibniz es mas intuitiva que las demás, pero a parte de eso la única ventaja que le veo es la de expresarla como operador. Por lo demás, es mucho mas compacta la de Lagrange y cuando te enfrentas a un examen de una asignatura de cálculo, reduce significativamente el tiempo de escritura, sobre todo en desarrollos como la regla de la cadena.
Esto es como todo, para gustos colores.
Por cierto, muy curiosa la notación de Newton que aparece en la Wiki, no la conocía.
Una entrada muy interesante. Espero con ansia la de las integrales. 😀
Yo soy profesora de Física, y siempre uso la notación de Leibniz. Además hago hincapié en lo que significa, nunca: derivada de f partido derivada de t.
El significado es: derivada de la función f respecto de la variable tiempo t (en este caso).
Yo soy profesora de Física, y siempre uso la notación de Leibniz. Además hago hincapié en lo que significa, nunca: derivada de f partido derivada de t.
El significado es: derivada de la función f respecto de la variable tiempo t (en este caso).
Soy profesora de matemáticas.
El problema del alumno para derivar una función compuesta creo que no radica en la notación.Según mi experiencia, el problema está en identificar la composición de funciones, es decir , cuál de ellas va dentro de otra.
Una vez que entiende eso, la notación es lo de menos.
La notación de Lagrange es más cómoda si hay que evaluar en un punto la función resultante.
La notación de Leibnitz tiene un inconveniente añadido: hay que escribir más letras.
Mi experiencia de unos años acá es que los alumnos intentan ahorrar en escritura lo indecible.
Cuesta horrores que escriban la palabra «lim » todas las veces que hay que escribirla en un desarrollo, o que no escriban solamente «sen» obviando el ángulo.
Cuando se quejan diciendo que se sobreentiende, mi respuesta siempre es la misma: » al profesor de Lengua no le protestas cuando te corrige las faltas de ortografía».
Creo que me he desviado un poco del tema.
En mi opinión, redefinir explícitamente las funciones es el mejor entrenamiento posible para entender la composición, y en eso la notación de Leibniz ayuda.
Conozco bien la resistencia de muchos estudiantes a escribir, pero no es difícil convencerles de que la tinta es más barata que los errores.
Totalmente de acuerdo contigo.
Según mi experiencia, en ciertos campos es más didáctica la notación de Lagrange (como en el estudio de funciones de una variable) y en otro la de Leibniz (como en los temas de cinemática).
En todo caso, un artículo muy interesante.
Casi siempre uso la de Leibniz a la que agrego Euler cuando hago cálculo tensorial.
Si no me equivoco (y si lo hago, agradecería que alguien me corrigiese y me explicara para sacarme de mi error), ambas notaciones no significan lo mismo: La notación de Lagrange es una derivada (límite del cociente del delta de una función y el delta de la variable independiente haciendo que éste último tienda a cero) y la de Leibniz es un cociente de dos diferenciales. Sólo coinciden ambos cocientes cuando se aplican a una función de una variable.
En ambos casos f es la misma función, además, si f fuese una función de varias variables se utilizaría una notación ligeramente distinta al tratarse de una derivada parcial.
Aclarada esta posible confusión, ambos símbolos significan exactamente lo mismo.
Otra razón para preferir la notación de Leibniz: a mediados del siglo pasado Abraham Robinson le dio estatus de «matemática rigurosa» a los infinitesimales al probar que los hiperreales funcionan, por lo que multiplicar y dividir por infinitesimales ya no puede ser considerado un pecado capital 😉
https://en.wikipedia.org/wiki/Abraham_Robinson
https://en.wikipedia.org/wiki/Hyperreal_number
Saludos,
Ricardo
Excelente artículo. Preparo alumnos en forma particular en mi casa. Y si bien me inclino más por la notación de Lagrange, tomo muy en cuenta cual usan los profesores de mis alumnos en sus respectivas clases ; me adapto a ellas. Para funciones z = f (x,y) los chicos entienden mejor con Leibniz.
Saludos desde Argentina.
Cada notacion tiene sus ventajas, y sus inconvenientes. La notacion de Leibniz es mejor al principio, pero hace que la derivada parezca un cociente y no se ve el limite por ninguna parte, además de ser larga. Muchas veces en derivadas parciales se usa la variable independiente respecto a la que se deriva como subindice, esta notacion es mas corta y me parece mejor.
Por otra parte ¿Es intuitiva la notacion de sumas de Einstein? Claramente no.
En definitiva ¡¡Usa la notacion que necesites coñe!!
Saludos
Respondiendo a Pepe :» pero hace que la derivada parezca un cociente y no se ve el limite por ninguna parte, además de ser larga »
Es que la derivada es un Límite, y dicho límite aparece por su propia definición de lo que es la derivada.
Como comentario general :
En la materia de Física fundamentalmente se ven todas las notaciones de derivación, por conocimiento propio (estudios de Física con ampliación de mates) el uso de cada notación depende básicamente del entorno en el que nos encontremos, esto es, de cuál nos conviene más o menos según la situación.
En las introducciones de Matemáticas estoy de acuerdo que después de introducir el concepto de derivada la notación que se suele usar es la de las primas (Lagrange) supongo principalmente por una cuestión de comodidad.
Por otro lado es evidente que la notación de Leibniz es la que tiene un significado físico directo, al diferencia del resto.
No obstante, en física en general la notación de Leibniz es la que se usa menos porque es más larga de escribir y a la hora de estar manipulando ecuaciones diferenciales digamos que no es la notación más manejable ni la más agradable de visualizar.
Un ejemplo, para resolver una ecuación diferencial de forma analítica (en caso que dicha solución exista) típicamente la ecuación se escribe en primas.
x» + w²x = 0 (ec. del oscilador armónico simple)
Con Leibniz esto se escribiría así, algo más engorroso:
d²x/(dt)² + w²x = 0
Por lo tanto, es usual hacer todas las manipulaciones y derivaciones en la notación de primas y luego pasar a la notación de Leibniz para la separación de variables y la solución final.
En análisis complejo, Relatividad, etc también se usa la notación de Euler (superíndices para indicar el orden de la derivada y subíndice para indicar la variable respecto de la cual se deriva). Esta notación es particularmente útil cuando se trabajan con muchas variables y varios órdenes de derivación.
En ramas como la Mecánica, finalmente, también se utiliza la notación de Newton (puntos encima de la variable que derivamos para indicar el orden de ésta). Esencialmente, en problemas de mecánica analítica donde aparecen muchas ecuaciones diferenciales con términos cruzados, elevados al cuadrado, etc… resulta bastante útil.
Ejemplo curioso de esto, en los problemas de mecánica resueltos en el marco de la mecánica lagrangiana, recordemos que la ecuación del movimiento equivalente a la Segunda Ley de Newton en mecánica Newtoniana es la ecuación de Euler-Lagrange que, pese a su nombre, la ecuación se escribe en la notación de Leibniz. Para colmo, una vez que tenemos el Lagrangiano del sistema, se aplica la ecuación de E-L y las derivadas se acostumbran a denotar por la notación de puntos! (Newton).
Por lo tanto, en la variedad radica la belleza… siempre que todas las variedades nos lleven al mismo sitio claro.
Como estudiante de segundo se bachillerato no puedo estar más de acuerdo con este artículo. No sé derivar por el método de Leibniz, y por el método de Lagrange se me da francamente mal, al menos en las que son mas enrevesadas porque me pierdo. Sin embargo integrar me resulta muy sencillo (e incluso entretenido), cuando supuestamente nos enseñan que integrar es más difícil que derivar.
Quizá la evolución de tus habilidades matemáticas siga un derrotero parecido al de la Humanidad. Se sabe que los antiguos griegos resolvieron las primeras integrales (Arquímedes es el ejemplo que me viene a la mente pero quizá hubo otros). Los rudimentos de la derivada no llegarían sino hasta el siglo XVII con Fermat y no se convertirían en lo que hoy conocemos como derivada hasta Newton/Leibniz. Hay por tanto una separación de 2000 años entre las primeras integrales y las primeras derivadas.
Algunos autores para la enseñanza de su disciplina toman en sus libros el llamado «enfoque histórico» en donde se avanza por los temas de una manera que sigue en lineas generales su evolución histórica. En el libro Calculus de Tom Apostol se sigue ese enfoque y se enseña primero la integración.
Al menos en la carrera de matemáticas nos dan para las derivadas la notación de Lagrange pues la de Leibniz hace pensar en la derivada como cociente de infinitesimales, los cuales no se pueden definir en análisis estándar (el que se deriva de ZFC.) En cuanto a la integral usamos la de Leibniz pero sin el diferencial al final.
Pues yo paso de una a la otra según me resulte más cómodo. Por ejemplo, si tengo un cálculo con derivadas sucesivas respecto a sólo una variable mejor Lagrange, si tengo un cambio de variable de por medio denoto a una derivada con prima y a la otra con punto, si hay más variables pues a veces utilizo Leibniz aunque me resulta más cómodo indicar la derivación con un subíndice. O sea, que depende. Creo que la mejor notación es aquella en la que uno escribe menos, y eso depende del cálculo en concreto.
Pus con leibniz aunque desgraciada mente cuando estoy resolviendo una ecuacion diferencial debo colocarla con notación de lagrange ser’a por la costumbre de los libros de texto? no la verdad no se pero para lo demás leibniz ya que soy un bestia y todo lo demás es mas fácil jajajajajaj
Bastante interesante maestro, mas que para poder darse a entender de como saber interpretar cada una de las diferencias dadas por los co-autores de cada área, aun mas mas poder relacionarlos de manera mas directa de cada uno de ellos estableciendo una forma de como poder diferenciar a cada una de ellas. gracias.
Es cierto que la notación de Leibniz permite comprender mejor y usar como fracciones las derivadas e integrales. No obstante, el uso de la notación de Lagrange lleva a unas preguntas que recientemente ha hecho furor (relativo) dentro de las matemáticas, ¿existe un exponente no entero? ¿cuál es la derivada 1’5 de una funcion? Esto ya fué preguntado en el s XVIII pero ahora ha desembocado en el cálculo fraccional, que te invito a descubrir y tratar en el blog.
No tengo claro que el cálculo fraccional tenga necesariamente que ver con la notación de Lagrange (piensa que también se usan enteros para las derivadas de orden superior en notación de Leibniz), pero es cierto que se trata de un asunto interesante.
Curioso debate…
Una ventaja adicional de la notación de Leibninz en ingeniería es que quedan claras las dimensiones de las magnitudes. Las dimensiones de dos cosas que se suman o de los lados de una ecuación deben ser las mismas. Una velocidad es LT-1 , una aceleración LT-2, una viscosidad ML-1T-1. En notación de Leibninz todas estas magnitudes resultan mucho más evidentes y hay menos riesgo de meter la gamba (intenta simplificar términos de las ecuaciones de Navier Stokes sin prestar atención al análisis dimensional y acabarás sumando una presión a una aceleración)
Desde la didáctica considero que la notación de Lagrange tiene la ventaja de mostrar que el resultado de derivar una función es otra función. Esta nueva función tiene sus propias características que, al estudiarlas, nos permite conocer mejor la función original. La notación de Leibniz, claramente, la notación por medio de diferenciales, es mas intuitiva en cuanto al cálculo posterior. Para poder trabajarlo adecuadamente es necesario definir diferencial de una función: dy=f'(x)dx. En mi experiencia esta última definición es difícil de comprender si desde el inicio se trabaja con la notación de Leibniz. Sin embargo es un abordaje sumamente necesario para que la notación de la integración sea más comprensible.
Muy buena propuesta para el debate…
Me parto de la risa. Uno piensa que con el tiempo las cosas van mejorando, especialmente en las más importantes como la educación.
El año pasado mi hija estaba realizando segundo de bachiller y asistí, horrorizado ya que yo mismo había pasado por ello mucho años antes, a cómo la torturaban realizando cientos de derivadas de las funciones más exóticas y con las combinaciones más inusuales que puedan darse en la naturaleza. Esto no tendría mayor problema sino fuera porque o bien no les explicaron nada de lo que significa en realidad el concepto de derivada o bien quedó oculto en los cientos de folios con cálculos (que por cierto ahora realiza y desarrolla instantáneamente el wolfram alpha). Yo no quise decir nada porque los chicos van muy cargados de trabajo en esa época, pero se me caía el alma al suelo. Me consolaba pensar que sólo se aprende a operar a base de práctica.
Llegó la selectividad y en vez de una complicada integral sólo solucionable por algún arcano método les ponen un trivial ejercicio de física que involucraba ¡¡plantear una sencilla ecuación de segundo grado con coeficientes enteros y derivarla!!.¡ Ninguno de los alumnos fué capaz de solucionarlo!. No habían entendido nada de lo que significaba una derivada. Un sencillo cambio de enunciado los deja fuera de juego porque no entienden lo importante.
En fin. Todo esto viene a cuento de que para enseñar a los chicos tal vez no es necesario usar todo el rigor matemático que si puede ser necesario más adelante. La notación de Leibniz puede ser leida cómo: Lo que cambia la función cuando cambia la variable independiente. Como aproximación mental a la derivada en un punto incluso puede decirse: Lo que cambia la función cuando la x se incrementa una unidad. Lo importante es el concepto de estudiar el cambio, no el rigor o los métodos.
Estoy absolutamente de acuerdo. De hecho, escribí sobre esto mismo aquí.
Una pregunta ¿En una expresión derivada que expresión se le agrega para que sea una diferencial?